Solving Coordination Challenges with Multidisciplinary Design Optimization (MDO)

• 00:03:13 Introduction to MDO
• 00:06:03 Variable Types in MDO
• 00:10:53 Reformulating MDO Problems
• 00:14:43 MDO Architectures
• 00:15:43 MDO Problem Formulations
• 00:24:13 Exploring MDO Architectures
• 00:40:09 Example Problems & Implementation
• 00:42:49 Project Conclusion: Learning & Challenges

Executive Summary of MDO Architectures

Multidisciplinary Design Optimization (MDO) provides a structured way to coordinate diverse, highly interdependent teams, balancing system-wide performance with organizational realities. By clarifying the relationships between disciplines and choosing the right architecture - centralized for efficiency or distributed for flexibility - leaders can prevent costly coordination failures and improve project outcomes. The most significant value often lies in the upfront process of problem formulation, giving decision-makers a clear roadmap before they commit resources to automation.

For decision-makers, MDO is more than a computational tool; it is a powerful framework for aligning technical optimization with organizational design. In complex systems engineering, where traditional, sequential design can lead to suboptimal results and internal friction, MDO maps interdependencies, defines shared variables, and aligns coordination strategies with how teams actually work. This helps avoid the pitfalls of siloed thinking.

The strategic choice to be made is between centralized efficiency and distributed flexibility, with a well-defined problem formulation serving as the foundation for either approach. In this presentation, BlockScience Research Engineer, Peter Hacker, reviews four distinct MDO architectures, each representing a different trade-off between centralized control and distributed autonomy:

• All-at-Once (AAO)
• Simultaneous Analysis and Design (SAND)
• Individual Disciplinary Feasible (IDF)
• Collaborative Optimization (CO)

His research highlights three key insights for executives and system architects:

1. Architecture Trade-Offs: Centralized approaches (AAO, SAND) reduce computational inefficiency but require tighter organizational control, while distributed approaches (IDF, CO) preserve team autonomy at the cost of higher coordination overhead.
2. Upfront Investment: Success requires early effort to define system coupling and problem structure, conditioning both technical outcomes and organizational coordination.
3. Formulation over Automation: The greatest value of MDO often lies in problem formulation—clarifying interdisciplinary relationships—rather than in automated optimization alone. Identifying coupling variables, design variables, and response variables is central to this process, providing clarity even when full automation is not feasible.

Published Research (2024)

This post is developed using AI and a humans-in-the-loop and represents an ongoing synthesis of BlockScience research initiatives, reflecting our intention to 'work in public' and share internal discussions and findings with a broader community audience. With the participants' explicit permission, and in combination with an adapted transcript, selected slides, and additional resources the following research is presented in the video.

Abstract: Multidisciplinary Design Optimization (MDO) focuses on optimization problems spanning multiple engineering disciplines that are commonly encountered in the engineering design process of complex systems. To solve a MDO problem requires managing disciplinary coupling and balancing resource-intensive disciplinary analyses of individual subsystems to achieve an optimal design at the system-level. In this paper the basics of MDO are presented in Section 1 followed by a review of four MDO architectures in Section 2 including: All-At Once (AAO), Simultaneous Analysis and Design (SAND), Individual Disciplinary Feasible (IDF), and Collaborative Optimization (CO). In Section 3, two example problems - a geometric programming problem, and a propane combustion problem - are presented and reformulated to fit the four MDO architectures. Each problem formulation was implemented using python and solved. The paper concludes with a simple benchmarking analysis comparing example problems and architecture implementations across solution precision and the number of function calls to the disciplinary analysis. The findings of this architecture review and implementation highlight the importance of tailoring the MDO architecture decision to the specific MDO problem characteristics in order to optimize the design process effectively.

Video Transcript, Presentation Slides & Associated Resources

[00:00:21] Peter: This is a presentation on multidisciplinary design optimization and a conversation originating from a paper that I wrote. What is most interesting to me, and probably to the group as well, is considering how multidisciplinary optimization might actually overlap with BlockScience topics. When coming up with a topic for this research project, I drew inspiration from Jamsheed's 2024 presentation on Parameter Selection Under Uncertainty (PSUU) and MDO, as well as Kryz Paruch's work on PSUU and social choice, so I would like to give a shout-out; this is more of a sequel than paving new territory. The other motivation for me is that MDO is essentially a coordination tool; its primary use case at the moment is facilitating decision-making among engineering teams, and we have a meme about the importance of coordination.

[00:02:10] Starting with a walk-through of the paper and project that I worked on. A quick TL;DR is that I spent some time diving into MDO, learning about the basics of what it is and what multidisciplinary optimization problems entail. I then identified a few architectures that serve as solution strategies for solving MDO problems. Then, I found some example problems and implemented and solved them to learn about MDO problems at a high level and their solution methods. I will provide a brief introduction to some MDO concepts, discuss MDO architectures in general, and highlight the ones that I have focused on. Then, we can review some of the implementation details for the solutions and examine the results of my findings.

Introduction to MDO

[00:03:13] MDO stands for multidisciplinary design optimization. Discipline is a keyword here - discipline and disciplinary analysis. There are some important variable types in the general problem formulation for MDO problems.

1. Design variables
2. Response variables
3. Coupled variables

We will review those and examine one of the main use cases or value propositions for MDO as it relates to disciplinary coupling. and then consider interdisciplinary feasibility.

Multidisciplinary design optimization has been used mainly for solving optimization problems that span multiple disciplines. In this case, disciplines refer to different engineering specialties, such as structures, aerodynamics, or fluid dynamics, among others. And then discipline analysis relates to the models owned by those teams, such as fluid dynamics models or finite element analysis. In our case, the models that we deal with are often cadCAD models. The main goal for MDO is to improve the optimization when disciplines are coupled.

Challenges in MDO

[00:04:37] In real-world use cases where multiple engineering teams are working on the same project, there are a couple of main challenges that generally arise. First is this expensive discipline analysis. Some fluid dynamic simulations or finite element analyses can be computationally intensive, cadCAD models in our case. The second challenge is resolving disciplinary coupling, when one engineering decision affects another team's outcomes.

How do you resolve that? This is the coordination aspect of MDO architectures, which I think is interesting. Essentially, many MDO architectures and solution strategies focus on managing these two aspects. In the real world, how do you manage your expensive disciplinary analysis and resolve disciplinary coupling?

In terms of application, Aerospace has been the most prominent. Designing rockets requires expertise in various engineering specialties. These are just some example images of use cases that I also pulled. For example, the team designing the engine in the back of the plane, their models and their outcomes are highly influenced by the design of the nose of the aircraft, because all the airflow coming over the body ends up going through the engine; these are two highly coupled disciplines.

Variable Types in MDO

[00:06:03] Now to take a look at the variable types that we are referring to in MDO problems. The three variable types were design, response, and coupling variables. As an introduction to what those actually are, we can examine a single discipline analysis case; technically not an MDO problem yet, but it has two of the variable types: design and response. The following two discipline analysis examples are from Kochenderfer and Wheeler (2019)

Single Discipline Analysis

[00:06:26]And so we have our discipline analysis, which would be some sort of simulation. And the Y vector represents the response variable, which is what the disciplinary analysis produces. It is then sent to the optimizer to optimize a specific function. X is the design variable in this case, and the design variables are what the optimizer optimizes over.

Multiple Discipline Analysis Example

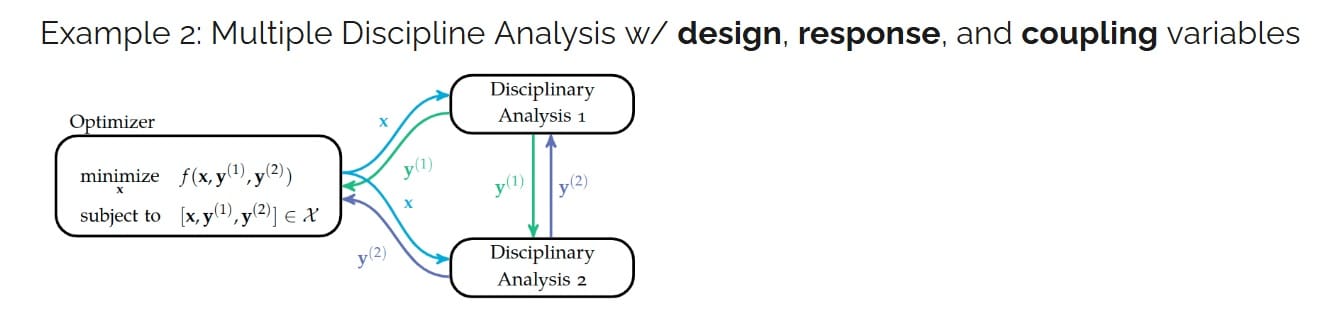
[00:06:50] And then to look at a multiple-discipline analysis example, this is where we introduce the coupling variables. And so the coupling variables are the variables that are shared between disciplines.

In this case, it appears that all the response variables are also coupled variables. However, in many cases, there might only be one or two variables that are coupled. We have the X design variables, which are controlled by the optimizer Y response variables, which are the output of the disciplinary analysis. And then the coupled variables are those that are shared between disciplines.

Disciplinary Coupling & Feasibility

[00:07:34] And then finally, to look at the disciplinary coupling topic and feasibility. Disciplinary coupling occurs when two or more disciplines share variables, as illustrated in the Multiple Discipline Analysis example. Disciplines can be highly coupled or less so, depending on the strength and number of connections that they have.

So, one discipline might be optimizing for its objective and come up with a value for the coupled variable that is not actually feasible for another discipline. So, if they were to pass that information to the other discipline, their model would fail or fall outside the constraints they have. So these types of dependencies need to be converged.

Discussion: Multi-Agent Influence Diagrams (MAID)

[00:08:34] Zargham: I am seeing here something that looks a lot like cooperative strategies for solving MAIDs, because so much of this is structural coupling in the decisions of actors within subproblems. So that graph that you are implying, which is a bunch of dependencies, is quite literally the ways in which the decisions of one actor, in this case an engineering team, affect the utilities or the objectives of another team.

And so, a framing of this that was popping into my head while I was looking at this is that there is a structural model. You could imagine modeling it as a MAID with the teams as the actors and the dependencies as the structural dependencies that you are showing here.

As opposed to a potentially adversarial or competitive game, you can almost interpret the MDO architecture as the scheme for cooperating in solving a joint utility problem where the various teams are actually not just distinct actors, but also members of a team of teams that actually has to solve the overall problem, rendering it effectively a cooperative game
-Zargham

Peter: Yeah. Definitely coordination, cooperation game similarities here.

Converging Disciplinary Coupling

[00:10:02] On converging disciplinary coupling, basically, different architectures have different strategies for achieving convergence and finding feasible solutions. But ultimately, why we want to consider coupling in the end is really because interaction effects do exist in the real world, and capturing those effects leads to a better solution.

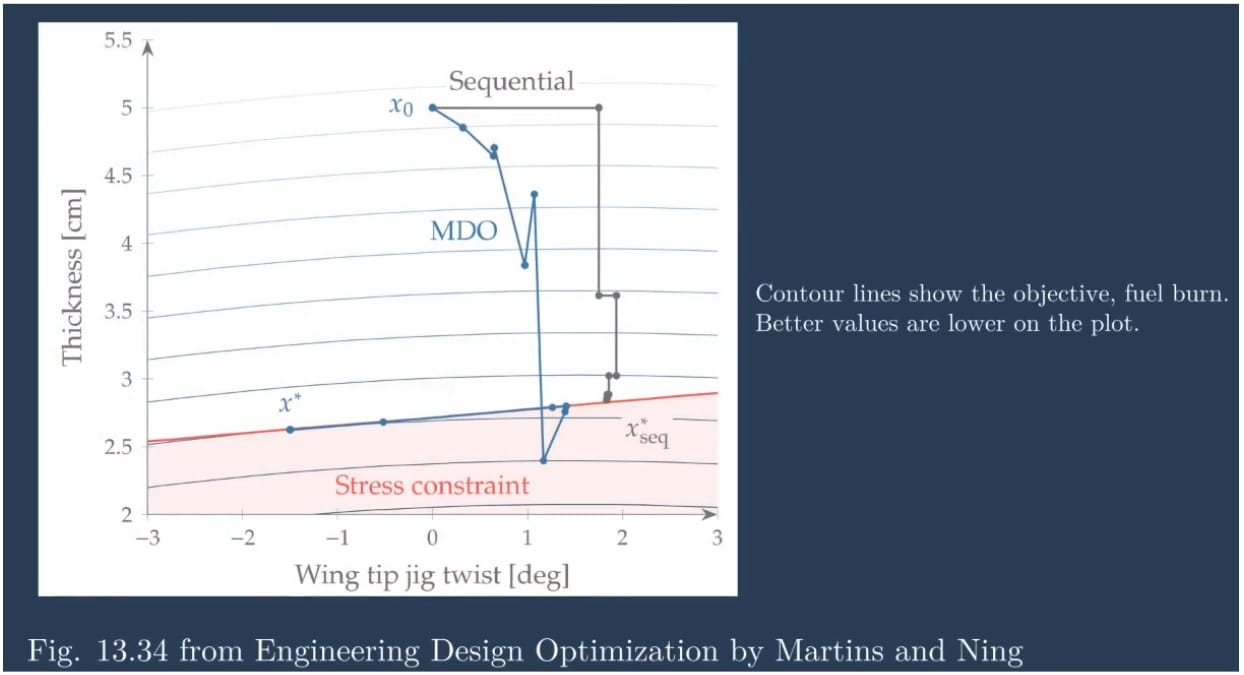
The example above from Martins, Joaquim and Ning (2022) compares an MDO method that accounts for coupling versus a sequential optimization method. I will not go into all the details of the chart, but basically, you can see MDO searches a little bit differently and ultimately ends up at a different optimal solution. Whereas the sequential optimization takes more like right-angle turns because it can only optimize one discipline at a time and ends up at a different solution point. So coupling is an important, real-world consideration.

Reformulating MDO Problems

[00:10:53] So to solve an MDO problem, you have to take whatever you are dealing with in the real world and formulate it as an optimization problem. There are different techniques to reformulate MDO problems - some are common across formulating any optimization problems, others are more specific to MDO.

Problem Structures

Common reformulation techniques to create different problem structures:

1. Adding variables
2. Adding constraints
3. Re-ordering Disciplines
4. Create subproblems by grouping or separating Disciplines

[00:11:26] Zargham: Is there a possibility that if we just look at this as a graph topology with a set of dependencies, is there a way of optimizing this giant universe full of variables with some sort of coupling or sensitivity to each other? And then partitioning the problem into subproblems becomes a matter of effectively clustering, possibly with some explicit hard constraints about what can and cannot be clustered together. It seems like there might actually be an optimization formalization of the problem of partitioning in the problem, so that you can then optimize it.

[00:12:16] Peter: Yeah, definitely. I think analyzing the coupling is a crucial step in designing a problem structure that will help you solve the MDO problem efficiently. And I would not be surprised if there are some ways to analytically optimize that. Although I do think in real-world applications, there might be context or knowledge that you have about the problem that, almost like a feeling or maybe from experience, these two disciplines are highly coupled, although you would not necessarily believe it, and it may be hard to quantify.

[00:12:51] Zargham: They could be coupled indirectly. So if the yellow node is really sensitive to the blue one and the blue one is really sensitive to the black one, in a way that leads to a sort of net high influence of the things that are not directly linked. Also thinking about it from the perspective of conditioning optimization problems, whether mostly intuitive, mostly analytical, or even computational pre-processing...

...there is an aspect here where processing the problem through even a very bespoke human process, resulting in a sufficiently well posed and well conditioned optimization problem, will significantly improve the performance of the computational methods.
Zargham

[00:13:31] Peter: I think that is definitely true here too. So, creating problem structures, obviously, there is a lot you can do in terms of creating problem structures.

Solution Strategies

And then solution strategies. How do you actually solve those problem structures? Solution strategies include choices for:

• System-level optimizer
• Subsystem-level optimization (if applicable)
• Algorithms to resolve coupling (if applicable)
• Algorithm to handle all the above

MDO Architectures

Monolithic vs. Distributed

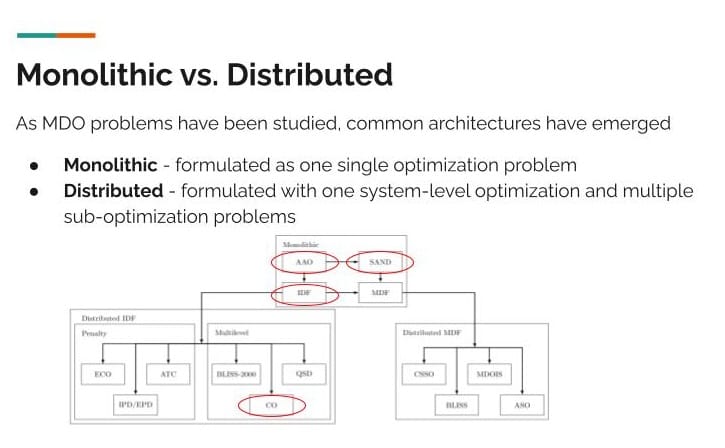
[00:14:43] As MDO problems have been studied, some common architectures have emerged and have been organized and classified in the literature and analyzed. This diagram highlights some structure of how the different architectures are organized. I circled the four architectures I explored within this research project. I started with the three monolithic architectures, and then I was able to get to a distributed one. Monolithic versus distributed is the main distinction in architecture type.

1. Monolithic is where you formulate a single optimization problem.
2. Distributed is where you formulate a system-level optimization problem and a subsystem-level optimization problem.

Naturally, the distributed architectures are more complicated to implement but they might be more realistic for real-world problems where you have multiple disciplines.

MDO Problem Formulations

[00:15:43] Before we jump into the architectures - the general MDO problem formulation is very abstracted, but basically the goal is to minimize the subjective function.

• We have the design x and response y variables.
• Subject to a feasible solution for all the disciplines m.
• Then F sub i represents a disciplinary analysis for discipline i
• The constraint shown is essentially enforcing interdisciplinary feasibility

This is the general form for MDO problems.

Referencing Generalized Dynamical Systems (GDS)

[00:16:21] Jamsheed: This is really nice to see because it gives you this understanding - as Zargham just alluded to - the notion that we have like a MAIDS component here, where we are thinking about that as a cooperative interaction between these different objective function subproblems.

But there is also a GDS aspect here, especially with regard to that capital X, you could even stick a subscript i on to that and say, the feasibility conditions, they have to have response variables and the design variables that fit for each one of the different sub-disciplines across the board. Such that - and this is the nice thing about that following representation - such that you have an invariant surface that you want to sit onto. And that is that capital F sub i, essentially an invariant.

And basically what you are saying is, "Hey, look, for all of these different choices, these things have to match up so that we actually have a larger set". And that is very much a GDS style kind of updating procedure where you would be looking for a particular criteria that you want to assess whether you want to throw out different types of design and responses. But that invariant surface still needs to be there for all of the things that it has to satisfy. I think that is quite a nice synergy that appears here.

[00:17:22] Zargham: Yeah. If I riff on it even further... if we introduce this X of i, you also can imagine certain kinds of variables that are effectively in the dimension of the edges more explicitly. So you have, again, X here is the state of the design variables for the whole system.

But insofar as we have this F of X, F of X Yi and we also have X sub i, I would argue maybe sub j, so that we do not have a strict assumption about the partitioning of the problem between the design variables and the response variables. But there is a lot of distributed optimization that has graph structure.

Without overly plugging my own dissertation, I spent most of my dissertation chasing problems which have underlying network structure. And once you integrate some of the GDS stuff, which allows for dynamics and characterization of constraints or objectives in terms of invariance, I think there are some really interesting ways in which this problem could be distributed more widely. Or just computed more efficiently if you have an explicit encoding of the network structure, and you can take advantage of that network structure to avoid, say, invoking expensive sub-optimization problems more often than you need to.

[00:18:42] ANON: Yes. This is pretty cool, Peter. So in my world, I would call this a bilevel optimization problem, right? You have a core objective. You have a set X, of your first level. Sometimes we call it the leader and the follower. So the leader is the upper-level optimization problem. And then you have the Fi of x, y, which is the follower in this case, right? This is the inner optimization problem that happens to be part of your constraint set. And something that actually is pretty useful across so many applications. But it comes with the difficulty that it is again about level optimization problems, which is sometimes very hard to solve.

And so I am just wondering if we have an adverse structure that is friendly and that has some nice structure that we can take advantage of and solve easily, then that may make things easier. Actually in my second paper, I had an optimization problem similar to this one. And that is why I am telling you it was pretty hard to solve... I see that you guys were talking with NASA about these types of problems and am just even wondering how they are trying to solve these types of problems to the scale that is needed.

NASA Model-Based Engineering Environment Team

[00:20:02] Zargham: On the NASA side, we were talking with some folks from the MBEE team about how you keep track of and access KOI like knowledge organization infrastructure, around models and functions, and their maintenance, mutation, safety, and stuff. We talked a bit about MDO because there is a project that Jamsheed presented on last year, which has some overlaps within their team structure. Because at NASA we are talking to the people basically doing open source software build for model-based systems engineering.

And even though the conversation started from a KOI MBEE perspective, we touched on MDAO and they expressed that they would have brought some other people if we wanted to talk about that. Which sounds like it is the case here too, right? If we had gone into that [conversation] with a less KOI-focused discussion, we probably would have invited Peter and ANON. So keep an eye on where those conversations go, currently in the shape of "we made some friends" because they do MBSE and open-source software, and we do MBSE and open-source software, albeit with a slightly different focus. We are talking to people at NASA at the level of knowledge sharing and learning.

[00:21:25] Peter: That is an interesting point about the network structures. And then in terms of solving these in the real world, that was one of the learnings that I was going to get too - knowledge of the real world problem is essential in order to be able to formulate and solve a problem. The value proposition for MDO is in the real world where you have these crazy large disciplinary analysis models that are highly coupled so you really do real world problems to be able to apply and see the value.

Actionable Insights from Decentralized Science (DeSci) Report

[00:21:58] Zargham: My intuition is that this is very actionable, even on some relatively simple problems, as soon as they cross the threshold into more than one subsystem. I will give you an example from the DeSci report that we have worked on.

Report Excerpt: This report guides readers through the systems engineering process, in order to provide design recommendations for a microeconomic model, a macroeconomic model, and subsidy programs for the DeSci Ecosystem. It begins by describing the DeSci Ecosystem's Animating Purpose and Stakeholders, then analyzes its Environment. It then offers a high-level overview of the project throughout all five stages of the engineering life-cycle, before focusing and the Requirements and Design of the new economic system

The design space, as I articulated it within the report, is three subsystems. One is a microeconomic model that relates to the day-to-day utility, to how it is used, the token access gates specific activities - and it is very much defined at a micro level. There is a macro level one, which has constraints related to supply and circulation. And there is a subsidy program type sub model that relates to how rewards from a pool of available funds are then deployed to drive specific objectives within the system and that is actually arguably the basis for an MDO problem.

And although I do not think we are going into a simulation phase on that project because they need to take that architecture, that structure, and strategy and run with it. But if they were coming back to us and saying, "Hey, we need to build a simulation," it probably makes sense to build three independent simulators that focus on their discipline for the subproblem. And then, insofar as we know that they are coupled, we would want to take a tactic like this. And that is a three-subsystem problem. So I see this as very natural.

To round it out - to the points about conditioning and network structure earlier - if you start with the conceptual model and then the subproblems and then the ability to design optimizers, or at least simulations of the subproblems, and then you start worrying about coupling them, it is in the question of how to couple them that we also need to deal with things like conditioning.

And that might mean that the dependencies are directed, and we want to look carefully at them. It may also lead to rescaling variables or creating normalized representations. And I think there are a lot of interesting - again, needs to be done by people with domain expertise - but a lot of interesting opportunities to create sub-models and coordinate amongst them, rather than trying to unify some of these like big, gnarly models that operate at different scales or on different phenomena.

Exploring MDO Architectures

[00:24:13] Peter: Okay, cool...... so there were four architectures that I looked at. Three of them were monolithic, one was distributed. I am going to go through quickly and cover some of the differences to get an idea of how these architectures can be designed differently.

All-at-Once (AAO) Method

[00:24:28]The first is called the All-at-Once (AAO) method. It is very general and has overkill in terms of constraints, variables and control of the optimizer. Yet it is the most general MDO architecture, and it is formulated as a single optimization problem. With AAO we have several changes to the general MDO problem formulation.

First, we have one new variable that changes from the general formulation. It is this Y superscript t. These are coupled variable targets, basically copies of a coupled response variable. The copy is used in a discipline other than where it was generated as a response. Creating the copies is one change. Second, because we have the copies of the coupled variables, we need to add these consistency constraints to enforce that the copies remain equal to the original response variable. Also in this architecture is this discipline residual. The residuals here, the constraints are set equal to zero, to ensure that the solution is feasible for all disciplines. Residuals for disciplines 1 through m.

[00:26:24] Zargham: Can I throw a quick flag out there? Making the residuals explicit like this with the R sub i and equals zero is a nice way to make the solution more legible because it means there will be Lagrange multipliers explicitly for each of the disciplines. So when you go to solve this the Lagrange multiplier associated with each of the constraints script R sub i will tell you something about how much you might need to relax the constraints. Or just from a meta perspective, it is actually really important that those are broken out so that they each get their own multipliers.

Simultaneous Analysis and Design (SAND)

[00:26:39] Peter: Moving on to simultaneous analysis and design. One small change from the AAO architecture is that we remove 1) the coupled variable targets and 2) the consistency constraints, since they are no longer coupled. But because we are still optimizing everything all-at-once, we are still able to reach interdisciplinary feasibility with the same residual constraints. It is just a slightly smaller problem size making for a relatively straightforward step from the AAO to the SAND architecture.

Individual Disciplinary Feasible Method

[00:27:12] So this is called the Individual Disciplinary Feasible Method. In this architecture, the residual functions are removed, and we actually get to use the disciplinary analysis for each discipline.

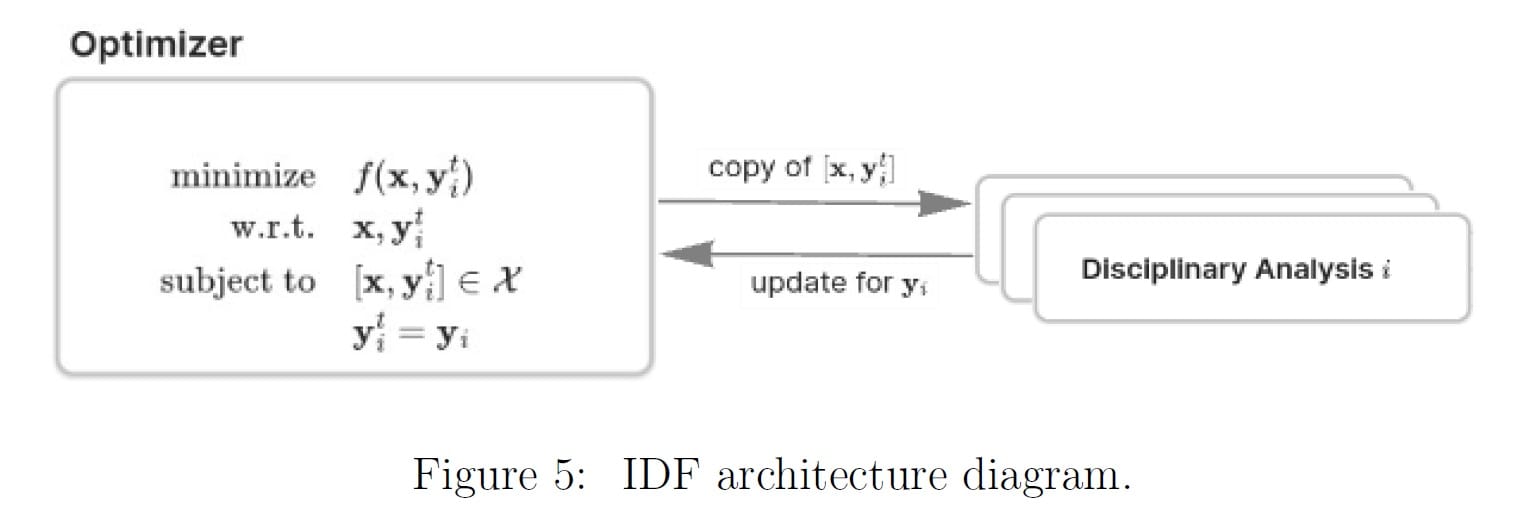
We can see in this diagram actual information flowing, it is not just a single problem statement. We have information flowing from the disciplinary analysis to the optimizer and back to the disciplinary analysis. There are benefits to the residuals, but it is not always possible to calculate them. So in cases like that, we would need an architecture that does not require them.

[00:27:48] Zargham: I would argue they [residuals] are not necessarily gone, that now they live in the disciplinary analysis. So this does not describe how the disciplinary analysis works, but if you were to reason about this once you have run it you should, at the very least be able to extract something about the trace of the local problem to tell you something about how it got to feasibility.

And one interesting thought about this is that the macro optimizer basically is enforcing this sort of, or is not the one enforcing feasibility at the disciplinary level. But again, that presumably is happening within the disciplinary analysis. I would argue this is already starting to be a properly distributed architecture and you are not just distributing the computation, you are distributing the responsibility for satisfying the constraints.

[00:28:42] Peter: Yep. Okay...And so then this architecture is able to run in parallel or the discipline analysis are able to run in parallel for this architecture since we are splitting them out. And I underlined here enforcing the consistency constraints are what enforced the feasible solution for the disciplines.

Discussion of IDF

[00:29:05] Zargham: I want to clarify what I was saying because I am hoping this is helpful that Y assertion is really, from my understanding, it is telling me that the Y i super t so the Y sub i in the macro optimizer is the Yi that came from the disciplinary analysis i. So that is like a binding, a thing that says, "Hey, we do not get to change this. This came from here." And so it is a way of connecting all of the individual disciplinary analysis response variables to the response variable that is in the macro optimizer.

But insofar as that response was generated by a process on the disciplinary analysis side that was feasible, is essentially - from the perspective of that disciplinary analysis- the burden of the disciplinary analysis itself, the thing that produced Y sub i .

And so what you are doing here in this individual disciplinary feasibility is doing what is effectively a hub and spoke type model. You have an orchestrator or coordinator in the optimizer, and then you have a bunch of subproblems and it is basically just saying "Do an iteration of the macro problem, then send copies of everything out to everyone. Let them do their things in parallel, collect up their results. Retrieve the results and do another iteration of the parent optimizer."

And you can think of that as a sort of hub and spoke model, right? Where it is just, "I do my thing, I tell everybody, they do their thing and then they send me back their results and I do my thing."

And my intuition here is that we are moving into something a little less centrally managed, but still ultimately solving a central optimization problem. So it is incremental. You are growing from the kitchen sink style, like canonical form "Hey, solve this by throwing all the computation at it" to something a little more specialized to something parallelizable to something that is arguably, distributed in a more flexible way.

[00:31:10] Peter: Yeah, and this is like the furthest it gets basically on the monolithic architectures before it gets even more distributed. So, that makes sense.

Collaborative Optimization (CO)

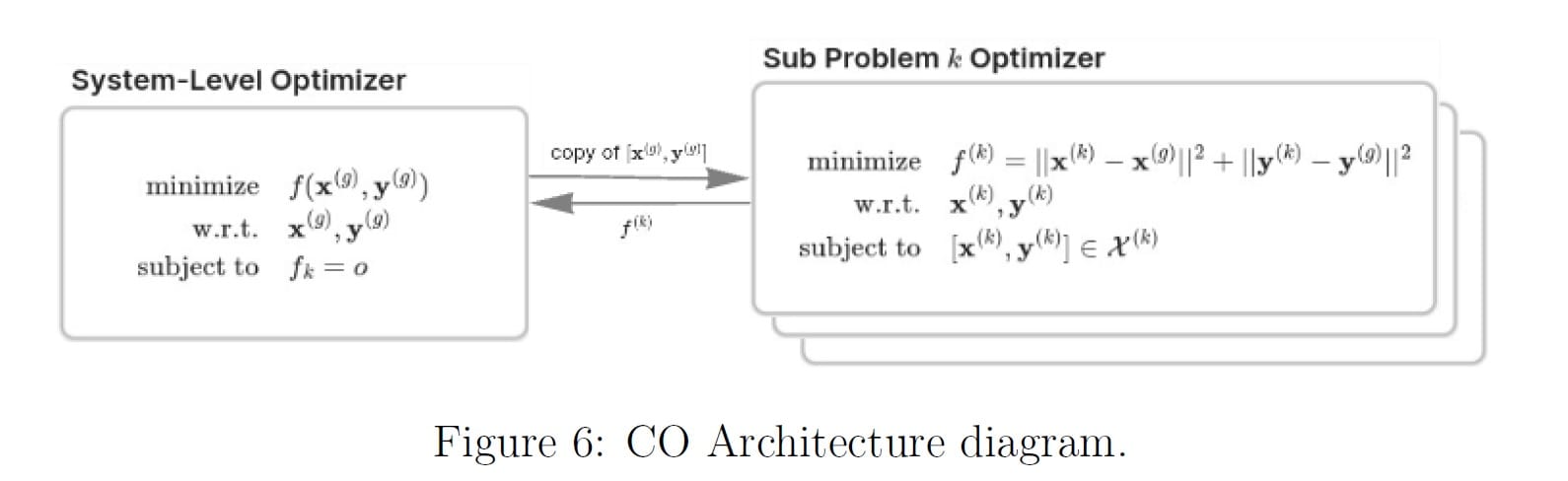
[00:31:17] And then the final architecture that I looked at, which is actually the first distributed architecture by those classifications earlier. We have our system level optimizer and subproblem optimizer. So I guess the main difference between this and the individual disciplinary feasible (IDF) method is that these discipline analyses are not necessarily their own optimization problems.

In this architecture (CO), these are sub-optimization problems where the objectives are actually where the interdisciplinary feasibility is enforced. So this architecture is reorganizing all of the disciplines in the problem into different subproblems. You can group multiple disciplines into a subproblem and the subproblems are responsible for optimizing the variables that are local to that problem.

[00:32:12] Zargham: So then that makes some sense. I think then what I am seeing that I missed on the first pass is just actually being really specific about effectively the observability and controllability in the design problem itself.

So when you run a disciplinary analysis and produce a response variable, you are essentially making observations about the consequence of a set of design decisions. So both the decision variables or the design variables, which are effectively your controllable parameters across the whole thing. And then your observable variables are effectively the response variables.
Zargham

And so this basically becomes a kind of distributed controls problem where you are making decisions about the design variables X. And then you are observing the consequences of the changes to the design variable X on the various response variables Y. But that observability is a consequence of the disciplinary analysis, but the controllability is a consequence of where the actual decision variables are.

And then this brings us back to this as a network problem, where you can effectively localize the various decision variables and response variables and the coupling can be weird. Like you could have places where if there is a network structure, the decision variable in subsystem i actually has most of its consequences on the response variables in subsystem j, and that is how you would start to use something like the controllability and observability matrix.

I am pushing in optimization as controls, vernacular here, but like actually the network structure and partitioning the problem might come from - at least for a big problem - understanding what is coupled to what, not just explicitly, but in terms of, input output response, like if there is high sensitivity of this response variable to this state variable. Then we have high coupling if there is that high sensitivity, even if they are not in the same partition or in the same disciplinary analysis.

[00:34:20]Peter: Okay. Yeah. Is that all analysis that would happen as like conditioning for the problem?

[00:34:25] Zargham Yeah, I think so. I am thinking about how to set the problems up and I guess I am coming at this from a perspective where I spent most of my dissertation work on distributed optimization. So I am making assumptions - whether they are right or wrong, they are baked deep in - but it seems to me that there is a lot of power here.

To your point earlier, the devil is going to be in the details at the level of the domain specific analysis, understanding the systems engineering problem as well as the subsystems and the way they couple. But part of the reason I like this so much is that it puts a little bit more formalism around the systems engineer's job because their job is not to develop the disciplinary model. Their job is to figure out how to synthesize and satisfy all of the disciplinary subproblems, such a way that the overall system can reasonably be expected to work as a whole. And that often gets fuzzy, right?

Like the subproblems can get really rigorous. And here is my model and here is my optimization. And everyone is arguing for the objectivity of their results. But then when you try to put it back together, it is still human-y and you are like, "Argh, but like this conflicts with that. You can not do that!" You have this integration process of the models of the design that can get messy and kind of returns to a very subjective, human conversation level.

I am not saying that is bad, you have to keep some of that. But what this does is it pulls it into this problem specification factoring, structuring, conditioning, so that you have a way of integrating various models together where all you need to know about them is what their decision variables like X are and what their response variables Y are and then you can have the factoring out of the constraints across the problem so that, these things do not need to be as tightly.

And again, I am a little biased towards this more collaborative optimization architecture because it matches up to some of my experience with distributed optimization. It is very likely that in any real applications that we would surface, it would probably end up looking more like the first [AAO] or second one [SAND]. Because I think we would end up with two to three disciplines. And the underlying challenge would be mostly around getting those systems to conform enough to talk to each other. Like if I have a micro model and a macro model, they literally run on different timescales.

And so that means if I want to optimize them together, I need a way of meaningfully interpreting the micro level models behavior, given a set of macro model expected dynamics and vice versa. And that is ultimately going to be the description of the coupling between the decision and response variables. And so most of it is actually going to be formulating this MDO.

And then in some cases we might not even need to run MDO. It might be that formulating the MDO is just the way to give an explicit and analytical description of the relationships between two or three models. And then if we end up doing an independent, human orchestrated version of an MDO process, we might still get better answers than if we had not started by formulating the MDO.

[00:37:47] Peter: I did read some articles about MDO. Some people just find the main use case for MDO to be to formulate the problem and not necessarily use the architecture for running the optimization problem to find a solution.

[00:37:59] Zargham: To be clear, I just think it is a table stakes, right? If you can not reliably formulate MDO problems, then you can not run them. But also, if you can not formulate them, you can not condition them. So there is a way that I think you have to go from formulating in the abstract sense, just as a set of relationships and understanding the couplings and whatnot, and documenting it. And if you can do that, then you can do things like possibly more analytic assessments of whether it is a well conditioned problem. Because given the intent, the computational intensity, I would hesitate to just throw a problem at this. You would want to spend a little bit of time to the best of your ability to structure and condition it.

And then you are basically running a kind of orchestration level process, which then runs a bunch of other processes. And since that is gonna be resource intensive and expensive, you want to make sure that you have a well conditioned problem and that you can do it manually, as a bunch of subproblems and look at how they relate to each other, before you commit the resources to run the actual MDO optimization.

And for us as BlockScience, I would say the first step is I would like to see us adopt some MDO type formulation for problems that have that are sort of multiscale or multidisciplinary in the sense that they are, they invoke models that do not operate on the same timescale, but are nonetheless, interacting through some of their variables, which we do have frequently.

And then we can worry about questions of conditioning and computational complexity and whether or not we wanna use an MDO strategy for actually running a, say, a PSUU [Parameter Selection Under Uncertainty] over a system that contains. And again, the simple case here is a micro model and a macro model, and if that works, then we could figure out how to make that more scalable and more reliable. But we really do not need to jump to there. We just need to actually express that problem as an MBO problem and think about how well or not it is conditioned. Yeah.

[00:40:00] Jamsheed: In the few minutes we have left, Peter, do you want to look at maybe one of the two problems?

Problems & Implementation

[00:40:09] Peter: Yeah, for sure...there were two example problems that I looked at. One was just a geometric programming problem, the other was some propane combustion problem.

Geometric Programming Problem Formulation

So this is the geometric programming problem, and the following slides show how the original problem is reformulated into an MDO problem.

So first [above], taking this and defining disciplines, assigning constraints, categorizing variables.

And then from the changes that I made on the first slide, the above slide shows some of the additional steps to reformulate it into the AAO architecture.

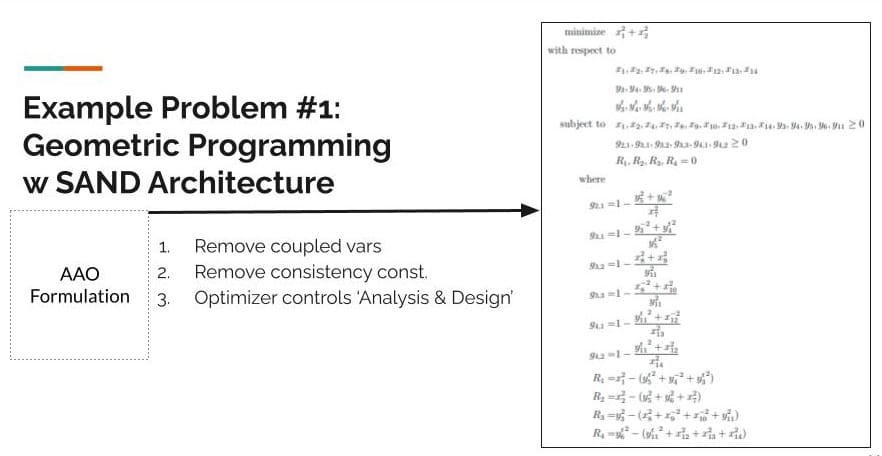
And above, reformulating it into the SAND architecture. Some of that stuff is pretty straightforward.

Propane Combustion Problem Problem Formulation

[00:41:02] Jumping to the propane combustion problem starting with the AAO formulation and making changes in order to reformulate it into the collaborative optimization (CO) architecture. So here, defining the subproblems and I am assigning the disciplines to these subproblems. It is a generic example problem. I do not have any context on how those disciplines may or may not be coupled, I just picked and assigned them and then formulated the problem.

Example Problem Implementation

[00:41:43] And then in terms of implementing and solving them all the three monolithic architectures are implemented and solved, using any optimizer - I think I used SciPy. But the collaborative optimization architecture as we noticed there is actual like subproblems that need to run. So the way that I implemented that was basically just within the constraints of the system level optimization problem embedding another optimizer to run. That was the MDO formulation implementation.

Data Analysis

[00:42:14] Peter: As for the analysis the data was as expected. There were two metrics that I looked at - solution accuracy and disciplinary analysis function calls.

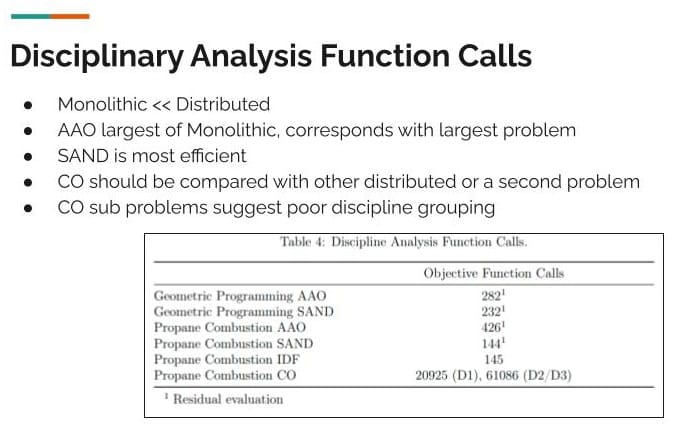
One of the key performance factors for solving an MDO problem is how many times you have to go back and query the discipline analysis because that is the expensive part. And for these example problems the monolithic architectures had a lot fewer function calls than the distributed architecture. AAO was the largest problem, so it took the most function calls, SAND was actually the most efficient.

Project Conclusion: Learning & Challenges

[00:2:49] Basically, the conclusions of the project were that the performance was as expected given the problem structures. So nothing too crazy or interesting on the implementation and data analysis side of it. But I think my main takeaway is that there is a lot of pre-work, work that goes into formulating the problem and understanding how problems are coupled before any of the implementation happens. Understanding the context of your real-world problem is important for producing a good solution. And from this experience, I discovered that the pre-work is way more important than the last few steps of implementation and solving.

[00:43:33] Jamsheed: Did you get a feeling for whether or not the OpenMDAO is a way to go in terms of helping that pre-filtering step? Or is that coming later in the process?

[00:43:41] Peter: I would say it is later in the process. So, it is after you have formulated and designed your problem with an architecture, then you use OpenMDAO to implement. It definitely helps, especially with gradient-based optimization it is incredibly useful. But that is a later step.

I am obviously interested to see how this could be useful for BlockScience, actually applying it to a real world use case. Because in my opinion the value proposition of multidisciplinary optimization is in the real world, coordinating teams with expensive disciplinary analysis and highly coupled disciplines . This research was great for getting an intuition about the architectures and the problem design but it would be awesome to see how some of this looks in the real world.

References

Gray, J. S., Hwang, J. T., Martins, J. R. R. A., Moore, K. T., & Naylor, B. A. (2019). OpenMDAO: An open-source framework for multidisciplinary design, analysis, and optimization. Structural and Multidisciplinary Optimization, 59(4), 1075-1104. https://doi.org/10.1007/s00158-019-02211-z

Hacker, P. (2024, July 31). Multidisciplinary Design Optimization: Architecture Review and Implementation. https://zenodo.org/records/15864586

Kang, N., Kokkolaras, M. & Papalambros, P.Y. Solving multiobjective optimization problems using quasi-separable MDO formulations and analytical target cascading. Struct Multidisc Optim 50, 849–859 (2014). https://doi.org/10.1007/s00158-014-1144-5

Kim, H. (2001). Target cascading in optimal system design [Dissertation (Ph.D.), University of Michigan]. https://www.researchgate.net/publication/33984207_Target_cascading_in_optimal_system_design

Kochenderfer, M. J., & Wheeler, T. A. (2019). Algorithms for Optimization: Chapter 21 Multidisciplinary Optimization. In Algorithms for Optimization (First Edition). MIT Press, 2019. https://algorithmsbook.com/optimization/

Martins, Joaquim & Lambe, Andrew. (2013). Multidisciplinary Design Optimization: A Survey of Architectures. AIAA Journal. 51. 2049-2075. 10.2514/1.J051895.

Martins, Joaquim R. R. A. and Ning, Andrew. Engineering Design Optimization. Cambridge University Press, Cambridge, 2022. doi:10.1017/9781108980647. https://flowlab.groups.et.byu.net/mdobook.pdf

Paruch, K. (n.d.). PSuU & Social Choice. hackmd.io. https://hackmd.io/@hr53QgK2R-yCA552WWJmYQ/r1I8WKnep/edit

Tedford, N. P., & Martins, J. R. R. A. (2009). Benchmarking multidisciplinary design optimization algorithms. Optimization and Engineering, 11(1), 159–183. https://doi.org/10.1007/s11081-009-9082-6

Wang, C., Fan, H., & Qiang, X. (2023). A Review of Uncertainty-Based Multidisciplinary Design Optimization Methods Based on Intelligent Strategies. Symmetry, 15(10), 1875. https://doi.org/10.3390/sym15101875

Zargham, M., & Shorish, J. (2022). Generalized Dynamical Systems Part I: Foundations. WU Vienna University of Economics and Business. https://doi.org/10.57938/e8d456ea-d975-4111-ac41-052ce73cb0cc

Zargham, M., Sisson, D., Ben-Meir, I., Vandevoord, C., & BlockScience. (2024). Digital Public Infrastructure for Decentralized Science. In https://nodes.desci.com/dpid/275/v6 (DPID 275). DeSci.com. Retrieved September 18, 2025, from https://nodes.desci.com/dpid/275/v6/overview

Acknowledgments

This AI-aided work is part of a broader inquiry into the role AI can play in synthesis and sensemaking when wielded as a tool rather than as an oracle. It is based predominantly on the research of Peter Hacker, and with his permission, repurposed here with the assistance of AI tools, including Descript, Claude, ChatGPT, as well as humans-in-the-loop for technical and editorial review, and publishing. Thank you to Peter Hacker, Michael Zargham, Jamsheed Shorish, lee0007, Jessica Zartler and all meeting participants.