A Summary of the Paper on Bonding Curves as Configuration Spaces by Zargham, Shorish and Paruch
This article introduces the main sections & concepts from the paper “From Curved Bonding to Configuration Spaces” by Michael Zargham, Jamsheed Shorish, and Kris Paruch, published at the University of Vienna Institute for Cryptoeconomics. The paper builds on concepts established in Foundations of Cryptoeconomic Systems, and is expanded further in Economic Games as Estimators.
The paper “From Curved Bonding to Configuration Spaces” introduces the standard specification of a Bonding Curve — a mechanism for minting and burning cryptographic tokens in peer-to-peer networks. It explains the rules by which the bonding curve operates that lead to the unique property of conservation, which in turn limits the possible system outcomes. The fact of limited outcomes, also referred to as “Configuration Space”, is what makes bonding curves unique and interesting from a design perspective. The paper then explores a version of bonding curves called the Augmented Bonding Curve, which is specifically designed for the use case of funding public goods via native token economies.
“Bonding Curves are less about what they give you, and more about what they take away. The invariant between a supply of tokens and assets held in reserve could address many of the basic economic problems we regularly see in web3 token ecosystems. Constraints have a funny way of setting us free.” — Michael Zargham
Paper Abstract
“Bonding curves are continuous liquidity mechanisms that are used in market design for cryptographically-supported token economies. Tokens are atomic units of state information that are cryptographically verifiable in peer-to-peer networks. Bonding curves are an example of an enforceable mechanism through which participating agents influence this state. By designing such mechanisms, an engineer may establish the topological structure of a token economy without presupposing the utilities or associated actions of the agents within that economy. This is accomplished by introducing configuration spaces, which are proper subsets of the global state space representing all achievable states under the designed mechanisms. Any global properties true for all points in the configuration space are true for all possible sequences of actions on the part of agents. This paper generalizes the notion of a bonding curve to formalize the relationship between cryptographically enforced mechanisms and their associated configuration spaces, using invariant properties of conservation functions. We then proceed to apply this framework to analyze the augmented bonding curve design, which is currently under development by a project in the non-profit funding sector.”
Understanding State Space Representations
A State Space Representation defines the state of a system, and how it can change over time through state transitions. It is useful because it defines the system completely, and allows anyone to understand the system and analyze its dynamics.
As an example, consider the analogy of a chef cooking a meal in a kitchen. The state space representation of this system would define the state as all ingredients, tools, and people in the kitchen. While the state transitions can be thought of as the recipe for cooking the meal. If we froze time at any point, the system could be described in detail through state variables such as the number of vegetables or sharpness of a knife. We could also describe an example state transition: the chef decides to chop vegetables in half according to the “chop-with-knife” instructions in the recipe, therefore doubling the number of vegetables and dulling the knife slightly. A complete state space representation of this kitchen would allow anyone to understand and analyze exactly how the state can change over time as the chef combines kitchen tools with ingredients according to the recipe.
In the case of a Bonding Curve, the State Space representation includes:
- State Variables: Supply of Tokens, Reserve of Assets
- Agent Address: A wallet address
- Eligible Actions: Mint tokens, Burn tokens
- Mechanisms: Deposit-to-Mint, Burn-to-Withdraw
Furthermore, a State Transition occurs when a valid[1] combination of an agent address, action, and mechanism triggers a change in one of the state variables.
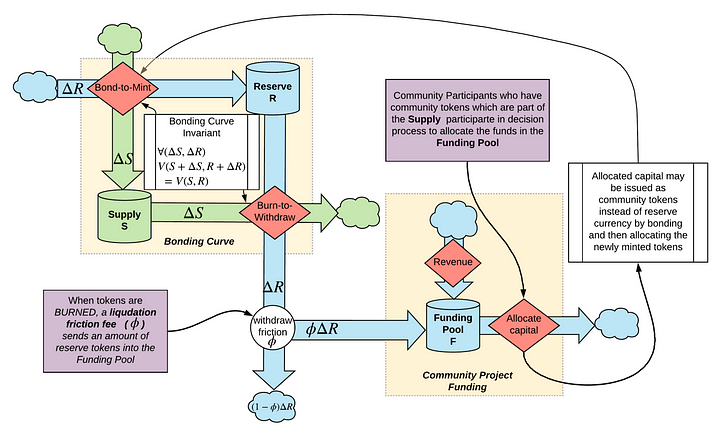
The image below demonstrates an example state transition that occurs when an agent decides to burn tokens using the “Burn-to-Withdraw” mechanism triggering a change in the “Supply of Tokens”. With the complete bonding curve state space representation offered in the paper, anyone is able to understand and analyze (i.e. through simulation) exactly how the supply and reserve amounts can change over time.
Designing Configuration Spaces
A Configuration Space represents every system state that is possible in a system as the result of a state transition.
An easy way to conceptualize configuration spaces is using your arm. It has certain points of rotation and flexibility (shoulder, elbow, wrist, fingers), but it also has certain invariants (the length of your humerus, or the rotational limits of your joints). By changing the angle and position of your arm, you can reach objects in different locations — everywhere that your arm can reach is in the configuration space of your arm. That itchy spot in the middle of your back is probably not part of its configuration space, which is why it is so difficult to reach!
When designing a system, specifying a configuration space is helpful for understanding the system dynamics. If the possible states that the system can reach are limited, then the number of potential outcomes for that system is significantly reduced. This allows for specific outcomes to be encoded (or excluded) in the mechanism itself by system designers.
In the context of bonding curves, the Configuration Space is meaningful because it is limited by a strict conservation function that requires a constant ratio of token supply S to the reserve asset R. This implies that for every token in existence, there is an algorithmic guarantee that some amount of reserve assets are available to back the value of that token. The ratio between supply and reserve, Vo, is the invariant which is calculated the moment a bonding curve is initialized[2] with supply = So, reserve = Ro and parameter = k (which determines how steep or flat the bonding curve is) with the following formula:
Once the bonding curve is initialized, we can generalize this same formula to all values of S and R (not only the initial values) and end up with the bonding curve conservation function:
This conservation function must remain satisfied for every combination of S and R for the entire life of the bonding curve (assuming no parameters are changed). And, with this conservation function, we can finally define the bonding curve Configuration Space, Xc, as all possible future system states X (i.e. any combination of S and R) where the conservation function from above is satisfied:
Visually, the configuration space of an initialized bonding curve using this conservation function is… a curve!

Application: Augmented Bonding Curve
The last section of the paper provides a full specification (including the State Space Representation, and Configuration Spaces) of a specific bonding curve application: the Augmented Bonding Curve (ABC). As the paper describes it:
“The augmented bonding curve is a minimalist design which binds a community stakeholdership token to a set of rights or privileges within that community, including but not limited to governance rights over a pool of funds controlled by that community.”
The ABC is a bonding curve designed specifically for the use case of helping Web3 communities fund public goods. It has roughly the same state space and configuration space as the original Bonding Curve — including, importantly, the same conservation property — but is modified slightly to include a discretionary community Funding Pool, and a withdrawal tax.
The withdrawal tax is represented in the diagram below by a “ɸ”. It is a percentage fee that users pay on a transaction when withdrawing reserve assets. The fee is sent to the funding pool which is represented on the right-hand side of the diagram. The funding pool is managed by the community of token holders and can be allocated to fund initiatives that support the shared needs of that community.
Thanks for reading, and don’t forget, this post is only meant to introduce topics covered in the original paper. For much more detail, including explicit state space & configuration space definitions, check out the full paper here:
https://research.wu.ac.at/ws/portalfiles/portal/18710394/zargham_shorish_paruch.pdf
This article was written by Peter Hacker and Jeff Emmett from the paper “From Curved Bonding to Configuration Spaces” by Michael Zargham, Jamsheed Shorish, and Krzysztof Paruch with feedback and edits by Hash Nabi.
Footnotes:
[1] Criteria that determine “valid” combinations of Agent, Mechanism, and Action are described fully on page 2 of the paper.
[2] Bonding curves are initialized through a process called a “hatch” which is described fully on page 8 of the paper.
About BlockScience
BlockScience® is a complex systems engineering, R&D, and analytics firm. By integrating ethnography, applied mathematics, and computational science, we analyze and design safe and resilient socio-technical systems. With deep expertise in Market Design, Distributed Systems, and AI, we provide engineering, design, and analytics services to a wide range of clients including for-profit, non-profit, academic, and government organizations.