Applying Control Theory to Cryptocurrency Monetary Policy
This piece is a deep dive exploration of the engineering design work carried out by the team at BlockScience, in collaboration with Reflexer Labs, focusing on parameterization of the RAI system prior to the mainnet launch which took place on Feb 17, 2021. Concepts covered include PID controllers, Governance Surfaces, parameter selection under uncertainty, controller stress testing, and safe system rollouts.
Preface
The web3 space has served as the foundation for rapid financial experimentation in many directions. Many of these projects seek price stability for their tokens (as any useful currency should), and often go about it in different ways. From external currency pegs to rebasing mechanisms, many attempts at “stability” have been attempted, but RAI is the first such token to use established control theoretical concepts towards a reflexive (or self-referential) price stabilizing token system. As opposed to existing systems which peg to fiat, RAI functions as a ‘dampened ETH’ because the stability controller attenuates price fluctuations caused by the underlying asset without requiring an explicit peg.
More specifically, by leveraging a proportional–integral–derivative controller (PID) controller in the design of the system, RAI provides a low-volatility reserve asset for the Ethereum DeFi ecosystem that is not pegged to any external asset. The depth of existing engineering practice on deploying PID controllers in everything from thermostats to cruise control offers us a solid engineering base from which to consider the design of RAI.
RAI as a Complex System
Optimizing complex systems infrastructure to balance the needs of multiple stakeholders is a feat of engineering design. It requires an understanding of system goals, constraints, and stakeholder needs, and thorough analysis of the trade-offs involved. Tools for modeling and simulation, like cadCAD digital twins, go a long way to helping us manage complexity and balance optimization to ensure preferred outcomes.
This requires a deep understanding of system goals and the parameters involved in the mechanisms we apply to achieve them. In this section we will examine the various goals of the RAI system, as well as what parameters are involved, both controlled and uncontrolled.
RAI Goals
The goals of the RAI ecosystem are the first consideration of the engineering design process. System goals ensure the cadCAD simulation parameters and metrics are aligned with the overall objective. The RAI project system goals are:
- smoothing of secondary market price movements without assuming a redemption price peg
- stability of the controller for a range of exogenous shocks
- graceful startup and shutdown of the Redemption Price adjustment if the secondary market violates liquidity requirements.
Our next step in systems design is identifying parameters, which fall into two categories: those that are under the control of the system (controlled parameters), and those that are out of our control (environmental parameters). Let’s dig into each of those parameter types for the RAI ecosystem.
Controlled parameters specify critical features that can be selected by system designers to achieve system goals. The RAI project control parameters can include:
- controller-specific parameters
- debt market-specific parameters
- pricing oracle parameters
Environmental parameters specify features that are external to the system, but affect the achievement of the system goals. The RAI project environmental parameters can include:
- the price of Ethereum
- the “external” demand for trades on secondary market (excludes “internal” demand for trades due to misalignment of market price and redemption price)
The metrics by which we measure the achievement of those goals is also important. Next we will look at metric/KPI selection: given environmental parameters, control parameters are selected in response to aggregations of KPIs that reflect system goals. The RAI project KPIs for each system goal include:
- responsiveness goal: reasonable arbitrageur and controller response times to different environmental parameter impulses
- volatility goal: statistical dispersion of secondary market price changes
- stability goal: measuring the relative frequency of stable vs. unstable paths across simulations
- liquidity goal: controlled slippage in secondary market
The Governance Surface
Cryptoeconomic systems and control systems share the phenomena that there are a set of parameters set by humans that encode trade-off decisions in the systems dynamics. In the case of cryptoeconomic systems, we call the parameters that are subjected to human oversight the Governance Surface.
It is important to make the governance surface explicit, and where possible it is important the effects of tuning such a parameter are relatively straight forward. All too often the concept of governance is used as a catch-all, assuming that humans will have the expertise, discipline and coordination to agree on changes to these parameters in the future.
In practice, one aims to keep the governance surface small in order to reduce the frequency and complexity of governance actions. Furthermore, upfront model-based systems engineering work can help inform the initial parameters to establish roll out plans and/or minimize the magnitude of future changes.
Understanding and Selecting the Controller Type
RAI is an innovative crypto economic system that uses a variant of PID controller as a means for maintaining market price stability. The PID controller is the most common class of controller. It makes use of a proportional term (P), an integral term (I) and a derivative term (D) for influencing the future values of a time series.
If you want to learn more about PID controllers and the basics of control theory, this 10 minute video from Brian Douglas is a great place to start.
One powerful feature of a PID controller is its ability to adapt continuously even when no predictions are available, as increasing errors tend to make it adapt with higher intensity. Specifically, the P term is a way of making sense of the immediate measurement, while the I term makes sense of the past. The D term is associated with the expected changes in the future.
Considering the D term, it is possible that by extrapolating into the expected changes, that the noiseless (idealized) steady state error rate is decreased at the cost of sensitivity to sudden movements. Derivatives in general are sensitive to noise and volatile measurements, which occur often in market prices. In an economic setting, the D term could become an attack vector.
Given these considerations, it was decided to focus the analysis on the P & I terms and set the D term to zero. Below, we provide a cursory overview of the kinds of analysis used to evaluate the options for RAIs parameters at launch.
Exploring P and PI Variants to Pretune for RAI launch
To date, RAI makes use of the P term (Kp) only for simplicity in the response dynamics; however, since proportional controllers are known to suffer from steady state errors, an integral term may also be desirable to include. While integral controllers deal with steady state error effectively, they are susceptible to ‘wind-up’ which is when the integral term accumulates causing bias in the control action. In order to counteract this, we must also consider an anti-windup mechanism. For this reason, the integral leak rate is incorporated into our parameter selection space.
The Malicious Whale Test
No experimentation with price stability would be complete without understanding the potential impacts of large token holders, or ‘whales’ as they are known in the cryptocurrency ecosystem. In the below scenario, we will consider the situation where a malicious whale named ‘Moby Dick’ buys up a large portion of the RAI supply and uses it to forcibly hold the market price of RAI at a constant.
In the example below, we have considered 5 variations of controller types available to us (positive vs negative Ki, and leaky vs non-leaky integrator, and zero Ki), and verify that, with a reasonable selection of parameters, the whale can expected to lose out to the controller in the long term.
The first visualization is to see what happens with the Redemption Price if Moby Dick holds the market price constant. As it is possible to see in figure 1 below, there’s a convergence of the Redemption Price going to zero during a 2 week interval on all tested scenarios, except for the one with negative Ki AND no leak term, signifying an infeasible parameterization choice.
The PI controller with a positive Ki term hastens the Moby Dick induced market crash relative to the proportional control, and the PI controller with a negative Ki term cushions the crash in hope that the attacker sees the writing on the wall and capitulates, allowing the system to recover. However, the leak term is critical because allowing the integral term to overpower the proportional term would equate to the controller capitulating to the attacker — something we cannot abide. Fortunately, there is an analytic bound on the relation between the leaky integral and proportional term that ensures this cannot happen.
How does this take place in the context of RAI economy dynamics? This happens because the controller automatically tweaks the redemption rate in response to the market price.
When a proportional controller (Kp only) or a PI controller (Kp & Ki) with the leaky integrator is chosen, the steady state dynamics include constant negative redemption rates, which is what we are aiming for in the RAI ecosystem. Notably, if we exclude the leak, the integral term creates a counter-productive acceleration effect. With a positive Ki, the redemption rate will accelerate in the negative direction, and with a negative Ki the redemption rate will accelerate in the positive direction. Neither of these PI (without leak) scenarios are particularly desirable scenarios.
The inclusion of the integral term in the absence of a leaky term can potentially make the RAI system unsustainable as clearly it allows for economic exploitation of users or make the token increasingly unusable due to the increasingly larger negative rates. Given that whale attacks are real concerns, this analysis indicates that the P controller is viable and the PI controller is viable only if the anti-windup leaky mechanism is included.
The Steady State Error Test
Another concern for RAI is the steady state error; specifically, it is possible for the system to achieve some semblance of price stability without closing the expected gap between the redemption price and the market price. In fact, the only reason integral terms were introduced into the control design space was to help eliminate steady state errors. Steady error issues tend to arise in the presence of noise or shocks.
In figure 3 below, the market evolves according to a Martingale process. We observe that the Ki term tends to introduce a bias on the redemption rate (see next figure), which may be small, but over time can compound into huge differences in the Redemption Price.
Figure 3. Even with proper parameter selection, the hourly redemption rate only varies by a small amount (<5e-9), but can still lead to large cumulative errors over time.
In figure 4, we can see the cumulative error behavior over time. The positive Ki without leak tends to increase the absolute error (larger magnitude negative error), while the negative Ki without leak tends to decrease the absolute error (smaller magnitude negative error), both measured relative to the P controller. The smallest absolute error is achieved for the PI controller with negative Ki without leak but we have already ruled out that design due to the malicious whale attack discussed above.
In our example the benefits of including the leaky integral term are small relative to the P only controller so further tuning would be required to meaningfully differentiate those two choices on the grounds of steady state error. For the time being, that means the complexity added by the inclusion of the I term is not warranted by the benefits to system stability in the near term, and more research in this direction is required before implementation.
Another important observation is runaway trends in the redemption price. The Proportional controller and the PI controllers with anti-windup converge, whereas the PI controllers without anti-windup run-away. The negative Ki term causes the redemption price to diverge (run away to infinity) and the positive Ki term causes the redemption price to converge to 0.
Selecting Parameters in Multi-Dimensional Systems Under Uncertainty
Iterating over the control parameters while making scientific sense of the sheer volume of data and complexity of the RAI system & interactions involves the usage of novel scientific methodologies.
Where the simple models above only considered the P(I) control logic, the models used for the analysis below include the collateralized debt positions of that back RAI as well as the liquidity pool servings as the secondary market (and price sensor) for RAI.
For that purpose, BlockScience developed the “Parameter Selection under Uncertainty” methodology for allowing data-driven informed decisions. A concise description of it as well as the associated steps and challenges is provided by this piece on Performing Parameter Selection Under Uncertainty.
Parameter Selection in RAI
In the following section we will provide some non-exhaustive examples of some of the computation experiments run on the more extensive RAI system model which includes the system of SAFEs and the liquidity pool (ETH/RAI Uniswap instance).
Scenario Testing
Our workflow stipulates a number of testing scenarios to connect system goals to measurable KPIs, and ultimately to the selected control parameters. The scenarios that were performed include:
1) ‘sanity checks’, to ensure that the Plant of the system behaves as expected; this considers the case when the controller is off and the sole source of uncertainty is the movement in the price of Ethereum,
2) shock testing, in which pre-determined changes in the exogenous processes are introduced and the responsiveness of the system measured, and
3) Trajectory sampling, in which Monte Carlo runs over many stochastic process realizations, and the KPIs reflecting the system goals measured and evaluated under a variety of environmental conditions.
“Sanity Check” Testing
A baseline scenario to test is one where the debt and secondary market systems act on their own, without the controller. This test is meant to ensure the “plant” model is working correctly before using it to evaluate the controller.
This sanity check replicates the ‘pegged-to-fiat’ controller by fixing the redemption price. In this case, the system should reach a state where Ethereum price movements are ‘passed through’ to the market price, and the redemption price is fixed at its initial condition (in this case, at the value set by Reflexer on launch, $3.14/RAI). The results of this ‘sanity check’ are given in figure 6 below:
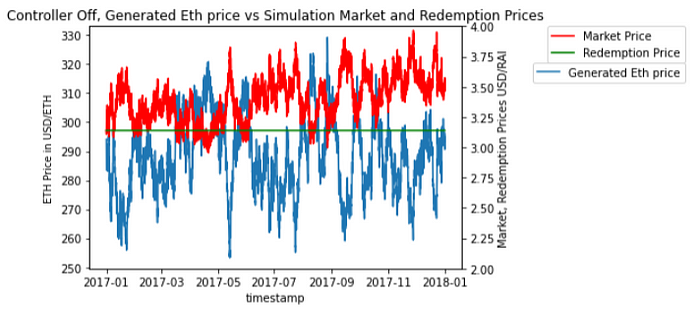
As shown in figure 6, the generated movement in the ETH price with the controller off creates a corresponding movement in the market price of RAI, with a slight upward drift (specific to the realization of the shock process realization for the ETH price). The observed dynamics are similar to those found in comparable systems such as single collateral DAI.
Shock Testing Attack & Failure Modes
As in any comprehensive system design, we need to understand the limitations of our system, and under what conditions it breaks down. Enter shock tests. Shock testing begins with a one-time change in a realized external process, such as the price of ETH, and examines the effect on the resulting system dynamics. Shock testing is especially useful to select parameter ranges which keep the system stable, i.e. keep prices and token balances from running off to infinity or zero.
“In systems design, you don’t really understand your system until you know where and how it breaks.”
— Dr. Michael Zargham
An example is the following scenario where we have a 30% sudden drop in ETH price after two weeks. As we can see, the scenario with Kp=2e-07 and 5e-09 has a runaway effect on the PI variables, while the ones that have values given by the parameter recommendations are maintained stable and bounded.
Recommended parameter ranges
Based upon the parameter selection under uncertainty workflow, we collectively determined that a P controller was the simplest and safest configuration for launching the network with the further observation that should we wish to further reduce steady state error an Integral may be added but ONLY IF the leak term is included and further satisfies the condition Kp > -Ki /(1 — 𝛼) where alpha is leaky integral parameter.
Figure 8 below is an example simulation using parameter values taken from the recommended ranges, where the proportional term is positive and the integral term is negative, exhibits stability — the controller acts to attenuate changes in the exogenous stochastic processes, such as the ETH price. In this case the Kp term is over 3 orders of magnitude stronger than the Ki term and the integral leaks 1/1000 of its value per period. The resulting system behaves comparably to the pure P controller at steady state (shown below) but has some additional capacity to knock out steady state error should they arise.
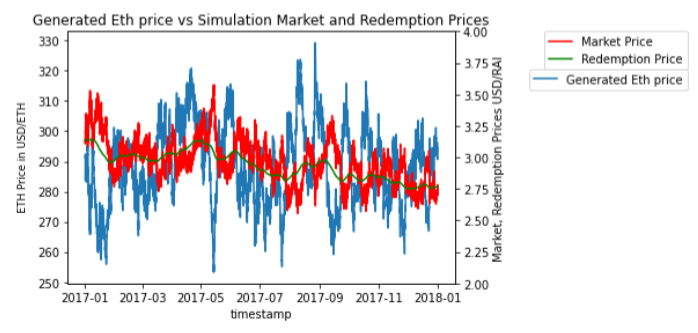
Progressive Rollout
When creating and deploying new financial systems, we need graduated testing and rollouts to ensure systems are safe before opening the floodgates to more users and more capital.
In October 2020, there was an incentivized mainnet test for ProtoRAI (PRAI), which was launched with low debt caps, used to test out system behaviors and inform the larger scale launch of the official RAI system. The intent here was to observe what happens at small scales with low stakes before full deployment.
The RAI network went live on February 17, 2021 with an initial configuration which had only the proportional controller Kp term. This system is exhibiting the desired behaviors and is consistent with the results we would expect in the proportional controller case.
Continuing to monitor the live data and integrate it with the systems models will reveal whether it is worth including the integral control term Ki and its leaky ‘anti-windup’ mechanism. This would add complexity to the system, but could also act to ensure longer term sustainability and thus facilitate governance minimization over the lifetime of the RAI system.
Governance Minimization
Attempting governance minimization by ignoring the governance surface is akin to getting into an autonomous car without the ability to instruct the car’s navigation about where you want it to take you.
In practice, governance minimization starts with a well defined governance surface, and follows with clear procedures about who, when and how parameters are changed. Successful governance minimization means making fewer, smaller, clearer changes, less often with less operational overhead.
It is rare for parameters to be totally uncoupled; more often the appropriate values are interrelated as we saw with Kp, Ki, and alpha (the leaky integral parameter). Models play an important role in monitoring system health because they can help disincentivize governance actions for their own sake, which actually put the system at risk, while conversely helping identify when action is needed, with enough early warning to plan, test and execute effective interventions.
Next Steps
Given that we have a fully functional model of the RAI dynamics and the mainnet launch, we have two natural next steps: Scaling the existing model so that it integrates with the live data for informing continuous monitoring. There are future decisions to be made as well as shocks and events to learn from in order to improve our understanding of the complex emerging dynamics around it.
Conclusion
Throughout this article we have summarized the engineering work that went into parameter selection for RAI’s stability controller, and aim to further educate and inform the Ethereum community about the importance of computer-aided design in complex systems.
By introducing the PID controller concept and how it is parameterized in the RAI ecosystem, as well as subjecting the system to batteries of shock and sensitivity tests to see how the system responds, we gain a better understanding of how RAI responds to various attacks and exogenous shocks that are outside of the control of the system.
Ultimately, the goal of the Reflexer team is to provide a low volatility, minimal governance, stable price asset for use in the Ethereum ecosystem. Despite uncertainty, those properties can be made reliable with a rigorous control theoretic foundation.
Stay in the Loop on Further RAI Research
Reflexer Labs:Discord: https://discord.com/invite/83t3xKT
Twitter: https://twitter.com/reflexerfinance
Medium: https://medium.com/reflexer-labs
BlockScience:Twitter: https://twitter.com/block_science
Medium: https://medium.com/block-science
Article by
Michael Zargham, Danilo Lessa Bernardineli, Andrew Clark, Jamsheed Shorish, and Jeff Emmett, with thanks to Stefan Ionescu and Ameen Soleimani for feedback and comments.


