A Series of Academic Analyses on GDS
This piece introduces a new three-part academic paper and supplementary video series on Generalized Dynamical Systems by Dr. Michael Zargham and Dr. Jamsheed Shorish.
Generalized Dynamical Systems (GDS) is a mathematical framework pioneered in the 1950s-60s that has been extensively researched and leveraged more recently at BlockScience for applications in the emerging area of enforceable contracts, such as may be found in Token Engineering.
In Part I: Foundations, emphasis is placed on the notation and definitions of Generalized Dynamical Systems and on conditions for representing dynamical systems within the GDS formalism from two conceptually related viewpoints based upon contingent derivatives and differential inclusions.
The next forthcoming paper, Generalized Dynamical Systems, Part II: Applications, will focus on applying GDS notation to example systems that already exist and proceeds to demonstrate what can be gained in design, operations, and governance work from a GDS model.
The final paper, Generalized Dynamical Systems Part III: Implementations, will focus on a framework specifically designed for the implementation of a GDS: the Complex Adaptive Dynamics Computer-Aided Design (cadCAD) framework.
Paper Abstract
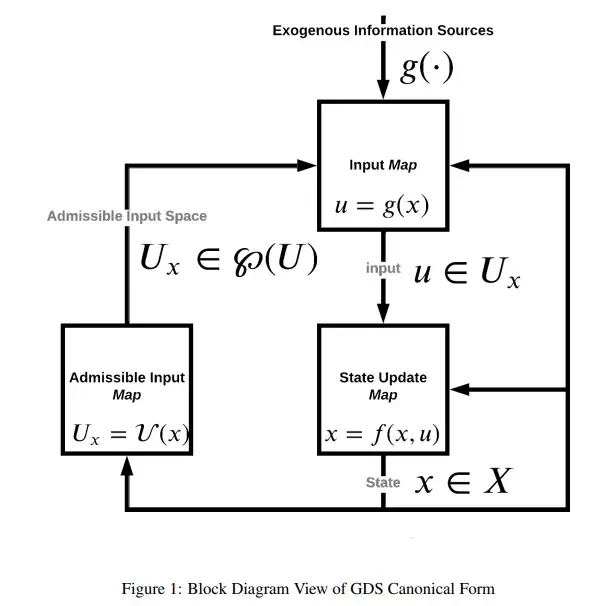
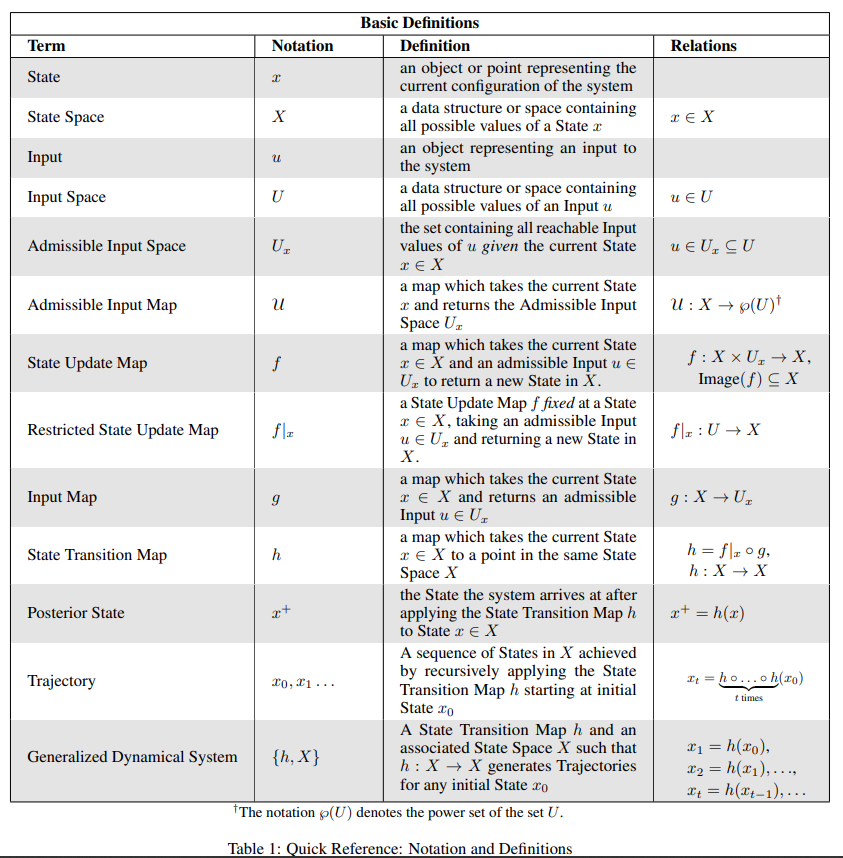
In the first of three works we consider a generalized dynamical system (GDS) extended from that initially proposed by [25, 24], where a data structure is mapped to itself and the space of such mappings is closed under composition. We argue that GDS is the natural environment to consider questions arising from the computational implementation of autonomous and semi-autonomous decision problems with one or more constraints, nesting into one framework well-studied models of optimal control, system dynamics, agent-based modeling, and networks, among others. Particular attention is paid to mathematical constructions which support applications in mechanism design. The contingent derivative approach is defined, along with an associated metric, for which a GDS admits the study of existence of state trajectories that satisfy system constraints. The system may also be interpreted as a discretized version of a differential inclusion, allowing the characterization of the reachable subspaces of the state space, and locally controllable trajectories. The second and third parts in the three-part series are briefly described and cover, respectively, applications and implementations, with the latter demonstrating explicitly how a GDS can be implemented as software using Complex Adaptive Dynamics Computer Aided Design (cadCAD) [30].
Read the full paper here: https://research.wu.ac.at/en/publications/generalized-dynamical-systems-part-i-foundations
4-Part Video Series on GDS
In a series of talks, Dr. Shorish grounds the GDS framework with a brief introduction and a simple, stylized, and tangible example of locating a crosswalk to:
1) illustrate the representation of a dynamical system as a GDS,
2) describe the principles of reachability and admissibility and how they influence the evolution of the dynamical system, and
3) introduce the notion of design goals that inform mechanism design and system controllability.
A Brief Introduction to Generalized Dynamical Systems
In this first video, Dr. Shorish gives a brief, high-level introduction to the GDS framework and how this mathematical representation can be used for representing time, actions, and admissible action sets and notation in complex systems, including uses for Token Engineering.
The Crosswalk Problem Reachability and Admissibility GDS Part 1: Representation
The Crosswalk Problem Reachability, Admissibility and GDS Part 2: Equilibrium and Existence
The Crosswalk Problem Reachability, Admissibility and GDS Part 3: Design and Controllability
In this fourth and final video, The Crosswalk Problem Reachability, Admissibility and GDS Design and Controllability, is about representing a system and also discussing its design and, ultimately, its controllability.
Acknowledgments:
Many thanks to Michael Zargham and Jamsheed Shorish for the hard work and great ideas that culminated in this research paper and many more fruitful collaborations in the future. A special thanks to the BlockScience team for feedback and support in developing these works.


