A Summary of the “Economic Games as Estimators” Paper on Bonding Curves as Estimators by Zargham, Shorish, and Paruch
This article introduces the main sections & concepts from the paper “Economic Games as Estimators” by Michael Zargham, Jamsheed Shorish, and Kris Paruch, published at the University of Vienna Institute for Cryptoeconomics. The paper builds on concepts established in previously published papers “Foundations of Cryptoeconomic Systems” and “From Curved Bonding to Configuration Spaces.”
TL;DR
The paper “Economic Games as Estimators” introduces a testing infrastructure for running numerical experiments on the bonding curve mechanism (as specified in the paper “From Curved Bonding to Configuration Spaces”) and discusses the experiment results. The experiments simulate a variety of market conditions and test whether a bonding curve mechanism is a good ‘estimator,’ meaning that it can effectively process mint and burn actions to generate a spot price that is a good ‘estimate’ of the true market price. The testing infrastructure includes a discrete event game designed around the bonding curve in which token holders continuously mint and burn tokens as their perception of the true market price changes. The game is designed in a way that minimizes assumptions about individual agent behavior, yet it is still able to produce a sample of true market price and therefore calculate an ‘estimation error’ comparing the bonding curve’s spot price to the sample price. This error metric can be analyzed and provides insight into whether the bonding curve mechanism accurately and consistently estimates the true market price.
These experiments put the bonding curve’s properties of conservation to the test to see whether the configuration spaces successfully limit negative outcomes in the face of changing preferences and unknown behavior from token holders.
Economic Games
Economic games are typically used by economists to analyze game theoretic outcomes. Discrete event games refer to a specific type of economic game in which state changes are event driven, and the system progresses one discrete step at a time (i.e., similar to a board game). One benefit of this game structure is that the iterative nature allows us to calculate system metrics that can then be analyzed for further insights. Discrete event games are applied as the framework for implementing the bonding curve experiments in this paper.
The Bonding Curve Game
The discrete event game designed for this paper was built around a bonding curve and token holder agent. The combined global state (bonding curve state + agent state) is driven forward by events as one discrete action of either minting or burning tokens occurs at a time.
In the diagram below, we visualize the high-level design of this discrete event game, starting with the event that would trigger a system state change — a token holder deciding to mint or burn tokens — then walking through one complete step:
- The agent’s private decision making process and the corresponding agent action trigger a change in the event driven system. This is a black box process, meaning no assumptions are made about the token holder’s behavior.
- The token quantities from the action can be observed, which reveal a realized price and trigger a state update for the bonding curve. The bonding curve machinery (i.e., the invariant/conservation property/configuration space described in the preceding paper “From Curved Bonding to Configuration Spaces”) goes to work and calculates a new spot price.
- The revealed realized price & newly calculated spot price are then used to calculate an error estimation metric.
The Sample Signal, Estimate, and Estimation Error metric
In step 2 of the diagram, it is described how the agent’s action results in two important price points: realized price and spot price. These are the two price points considered for the numerical experiments in the paper.
- Realized Price — The discrete economic game was designed intentionally to reveal this signal after an agent action. This price value plays a very important role in the numerical experiments as a sample signal of the true market price, since the true market price itself is unknown. You can think of collecting realized price samples as similar to recording the sticker price for a can of Coke at different grocery stores each time a customer makes a purchase. Since the theoretical true market price for a can of Coke is unknown/difficult to measure, the sticker price serves as a sample signal.
- Spot Price — This price value is calculated according to the amount of tokens in the reserve/supply pools and the exact bonding curve specification. The bonding curve is an estimator in this system because it produces a spot price that is an estimate of the true market price. This estimation capability is what the numerical experiments are testing.
Together, the difference between the sample signal and estimate gives us an important system-level metric: estimation error. This metric is calculated after each mint or burn action and can be collected/analyzed to draw conclusions about whether the bonding curve mechanism is a good or bad estimator of the market price sample.
The Simulation Implementation & Numerical Experiments
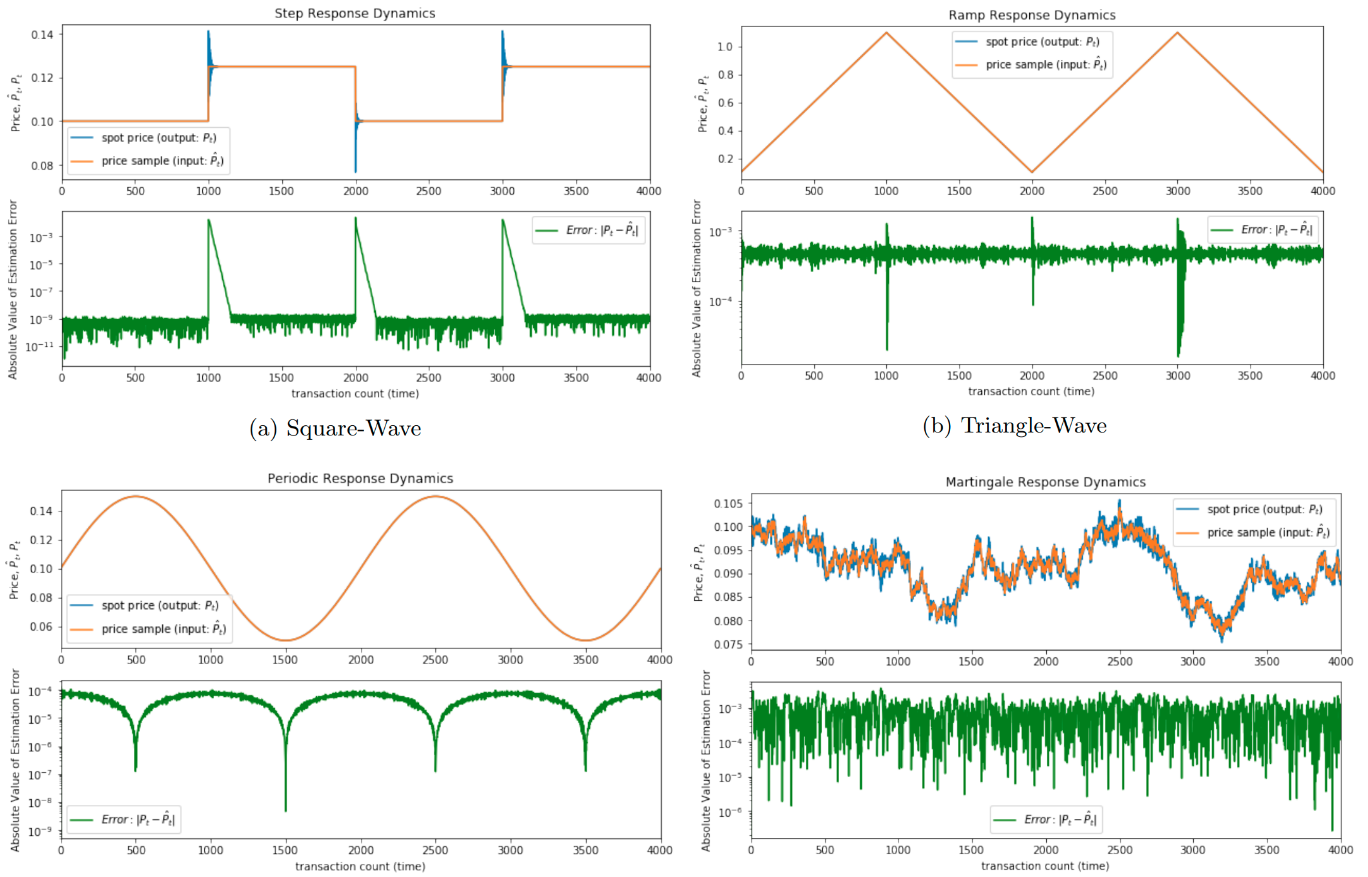
The goal of the numerical experiments presented in this paper is to test whether the bonding curve mechanism, when faced with a variety of price change conditions, produces a good estimate (spot price) of the true market price (of which, the realized price is a sample). Four scenarios of price change patterns are considered:
- Square-wave (deterministic)
- Triangle-wave (deterministic)
- Sine-wave (deterministic)
- Random-walk (non-deterministic)
The sequence of price values produced by these rules is not meant to be a prediction of actual price behavior, but rather a gauntlet of different price change patterns to pressure test the bonding curve’s estimation capabilities.
The model designed for the simulation has mostly identical components to the economic game described above; however, a key difference is that the simulation is implemented as an input-output system rather than an event-driven system. The input is called the driving process and is equivalent to the realized price. The output is the estimation error. This diagram walks through the high-level steps for one iteration of the simulation:
- Before a simulation begins, each price change pattern generates a sequence of price values. This is called the driving process and is a sequence of price values equivalent to the realized price. At the beginning of each iteration, a new price value from this sequence is taken as an input to the simulation.
- An agent action occurs after comparing the previous iteration’s spot price and the price value from the driving process (i.e., burn if driving process price is less than spot price, and vice versa). The amount of tokens involved in the mint/burn is the amount that brings the ratio of token reserve to token supply back in line with the new realized price.
- A state update is triggered by the change in token reserve and supply quantities, and the bonding curve machinery goes to work calculating a new spot price.
- Finally, the error estimation metric for this time step is calculated as the difference between the new spot price and the realized price from the beginning of the iteration.
After many iterations of mint and burn actions adjusting the token reserve to token supply ratio to match the realized price, enough estimation error measurements are taken to analyze the data and draw conclusions.
Conclusions
Numerical experiments like this are an essential step in validating mechanism design. The unique combination of discrete economic game machinery with control theory estimation techniques proved to be an effective design for producing scientific results.
In the end, the experiments showed positive results for the bonding curve mechanism as a price estimator. When plotting the data collected, we can see that the estimation error metric behaved differently with each price change pattern, but in general, the error converged consistently following price changes and did not accumulate over time.
These results should provide confidence that the mechanism will maintain its properties and continue producing accurate estimates of market price through many market conditions.
Acknowledgments
Thank you for reading! And don’t forget, this article is only a summary of the main sections and key concepts from the paper “Economic Games as Estimators.” To dive deeper into the specification of the discrete economic game design or for a much more thorough analysis of the numerical experiment results, be sure to read the original piece here: https://research.wu.ac.at/en/publications/economic-games-as-estimators-3.
This article was written by Peter Hacker with feedback and edits from Jeff Emmett, Lila Langsford, and Jamsheed Shorish.
About BlockScience
BlockScience® is a complex systems engineering, R&D, and analytics firm. By integrating ethnography, applied mathematics, and computational science, we analyze and design safe and resilient socio-technical systems. With deep expertise in Market Design, Distributed Systems, and AI, we provide engineering, design, and analytics services to a wide range of clients including for-profit, non-profit, academic, and government organizations.